
|

|

|
|
Measuring the Earth
If the Earth is round, we should be able to measure the curvature of its surface. Science tells us that water conforms to the curvature of the Earth so boats disappear in the distance as they sail over the curve.Perhaps a simple experiment could confirm the curvature. As a boat sails away, it sinks lower and lower, so if we measure how fast it sinks, we should be able to calculate the curve.
In 1838, Samuel Rowbotham set out to do just that on the Bedford Level, a straight six mile canal in Norfolk England. Rowbotham's experiment is simple and we can easily duplicate it along any beach with a clear line of sight.
|
The Bedford Level Rowbotham set a telescope eight inches above the surface of the water while his friend rowed a small boat over the six mile distance. Figure 1 at right shows the geometry we expect on the curved Earth. Table 1 gives values for W, E, and H. Rowbotham attached a tall flag to the transom to extend his measurement range, expecting the boat to disappear from sight after a mile or two. |
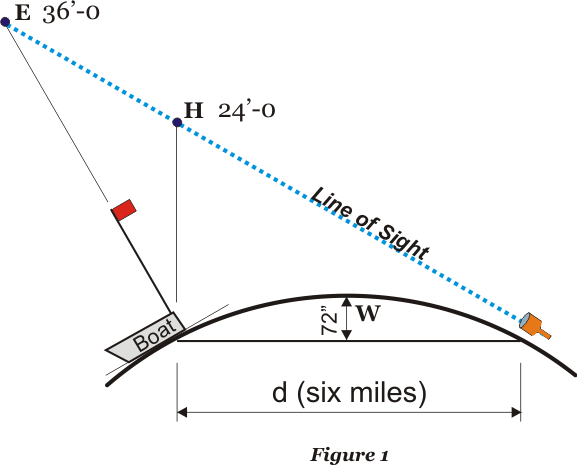
|
|
The boat did not disappear. The entire boat was visible for the whole six mile trip. But how can this be? If the telescope was level to the ground, the boat would be 23 feet below the line of sight. Even if the telescope angled "downward" the boat could not e seen because a six foot bulge of water would be between the telescope and the boat. Rowbotham concluded that he saw the boat directly as shown in Figure 2. But if this is so, the Earth must be flat! |
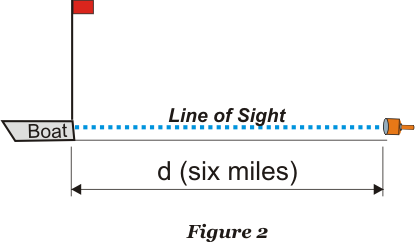
|
The Bedford Level experiment is well known (even Wikipedia weighs in) so you can look it up in many places. The Bedford Level experiment was repeated in 2016 by a large group and results confirmed Rowbotham's findings.
The Wikipedia article concludes with an obfuscatory and arm-wavey assertion that light curves along the river, quoting as proof an undocumented theodolite experiment where light traveled in a straight line.

|
|
|
|
|
|
|
|
|