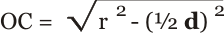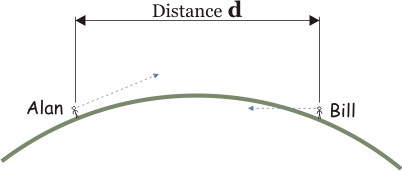
The Glass Ceiling
Chapter 7: Round Earth Math

Round Earth Math

Alan and Bill are standing on the surface of the curved Earth at some distance d apart.

Alan is standing straight up so his line of sight is parallel to the Earth.

Bill is leaning far forward so his line of sight points directly at Alan. Can Bill see Alan? We answer this question with a small amount of math.

To simplify the math, we assume that Alan and Bill are both treading water, so their respective eye levels coincide with the water surface.

Draw line AB from Alan to Bill, and mark its center point C. The water bulge between Alan and Bill, line CW, is r minus the length of line OC.

AOC is a right angle triangle. By the Pythagorean theorem:

r = (1/2 d) + OC .

so

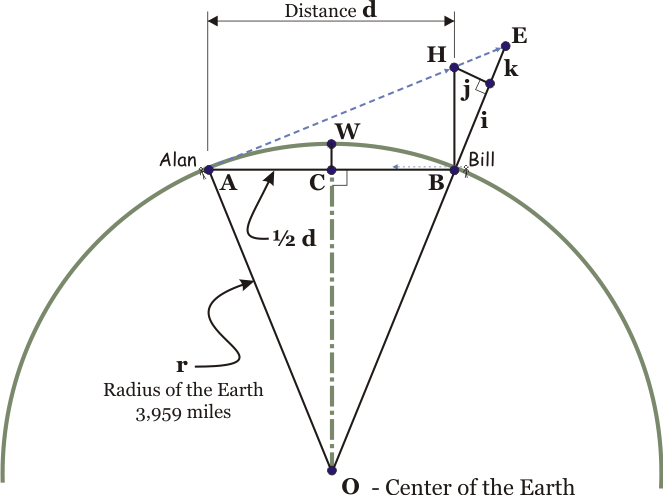
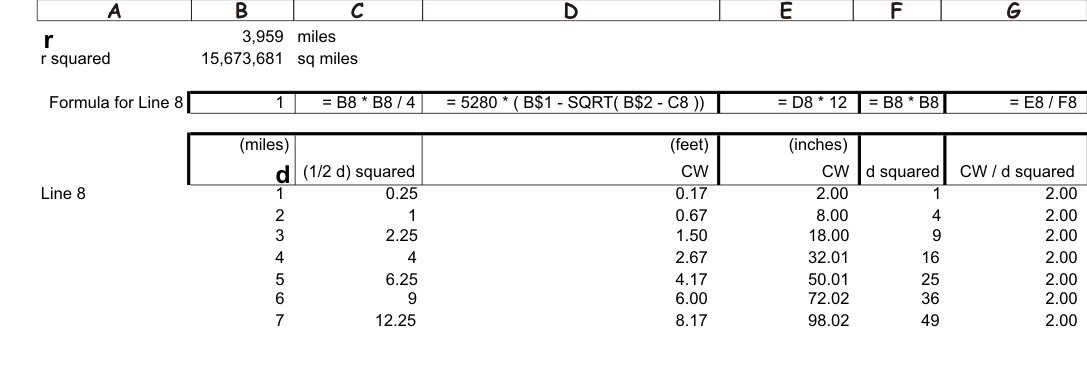
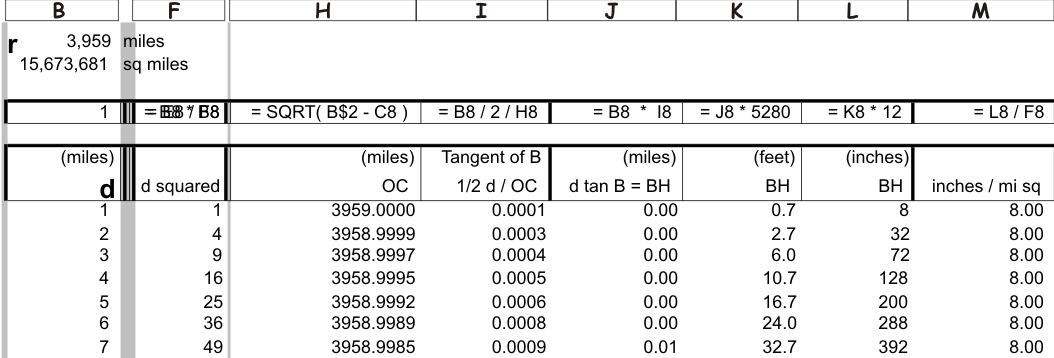
Placing the formulas in a spreadsheet as shown and replicating down, we make a table for distance vs height. As you can see the height of the water bulge is about 2 inches times the square of the number miles of distance.

The next question is how tall does Bill have to be before Alan can see him? If Bill keeps leaning forward, the answer will be given by the length of BH. If Bill stands straight up, the answer will be the length of BE.

Let's find the location of H. To do this, we have to solve the triangle ABH, This time we do not have the length of the hypotenuse but we know that angle H is the same as angle B because AH is perpendicular to AO.

We also know that the tangent of angle B is OC / 1/2 d so we extend the spreadsheet as follows:

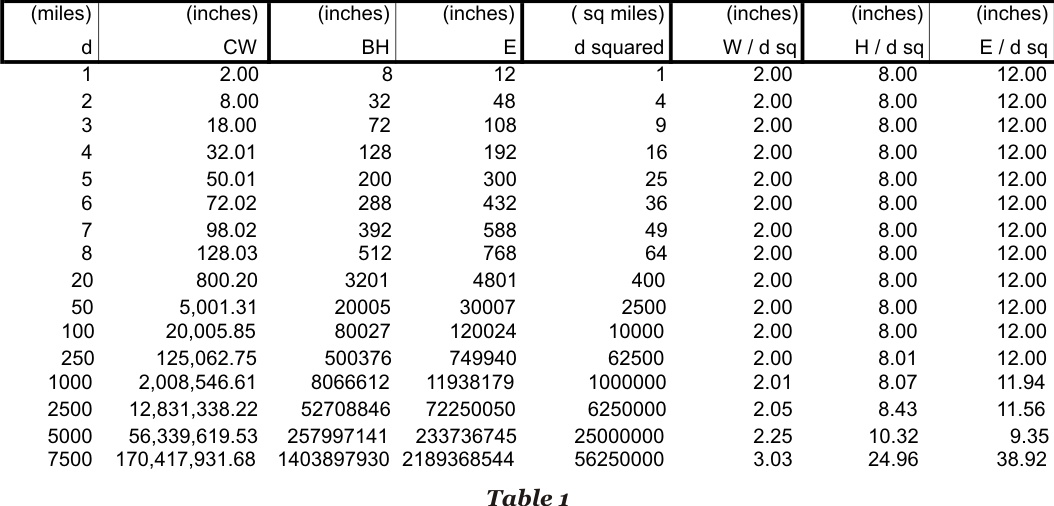
As before, the height in inches is relative to the square of d. H per mi sq is almost exactly 8".

To find the length of the line BE, we solve two more right angle triangles. The spreadsheet is wide after deriving j, i and k, so summary results are presented here for the three heights. The value is seen now in using the spreadsheet for the solution because we can replicate down to build a useful table.

This solution is not unique, but is chosen for simplicity as it uses only common trigonometry and can be performed with any spreadsheet or calculator. No trigonometric solution can be exactly linear because the Earth is curved, but as you can see, this solution can be considered exact for the first couple of thousand miles.
Back to ISS Contents Next: Bedford Level
Home Forum About Contact Us